Theoretical Foundation¶
This section briefly covers the underlying theoretical concepts upon which parameter estimation -and by extension kafe2- is based.
Basic notions¶
Measurements and theoretical models¶
When measuring observable quantities, the results typically consist of a series of numeric measurement values: the data. Since no measurement is perfect, the data will be subject to measurement uncertainties. These uncertainties, also known as errors, are unavoidable and can be divided into two subtypes:
Statistical uncertainties, also called random uncertainties, are caused because of independent random fluctuations in the measurement values, either because of technical limitations of the experimental setup (electronic noise, mechanical vibrations) or because of the intrinsic statistical nature of the measured observable (as is typical in quantum mechanics, e. g. radioactive decays).
When a measurement is performed more than once, the statistical uncertainty of the average of the single measurements will be smaller than those of each individial measurement.
Systematic uncertainties arise due to effects that distort all measurements in the same way. Such uncertainties can for example be caused by a random imperfection of the measurement device, which affect all measurements in the same way, and hence the uncertainties of all measurements taken with the same device are no longer uncorrelated, but have one common uncertainty. As a consequence, repeating a measurement will not reduce the uncertainty of the end result.
In most cases, measurements are affected by independent and by correlated errors. In order to make meaningful quantitative statements based on measurement data it is essential to quantify both components of all uncertainties, expressed in terms of their covariance matrix, or by the uncertainties and their correlation matrix.
Parameter estimation¶
In parameter estimation, the main goal is to obtain best estimates for the parameters of a theoretical model by comparing the model predictions to experimental measurements.
This is typically done systematically by defining a quantity which expresses how well the model predictions fit the available data. This quantity is commonly called the loss function, or the cost function (the term used in kafe2 ). A statistical interpretation is possible if the cost function is related to the likelihood of the data with respect to a given model. In many cases the method of least squares is used, which is a special case of a likelihood for gaussian uncertainties.
The value of a cost function depends on the measurement data,
the model function (often derived as a prediction from an
underlying hypothesis of theory), and the uncertainties of
the measurements and, possibly, the model. Cost functions are
designed in such a way that the agreement between the measurements
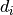 and the corresponding predictions
and the corresponding predictions 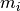 provided
by the model is best when the cost function reaches its
global minimum.
provided
by the model is best when the cost function reaches its
global minimum.
For a given experiment the data 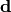 and the parametric
form of the model
and the parametric
form of the model 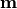 describing the data are constant.
This means that the cost function
describing the data are constant.
This means that the cost function 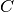 then only depends on the
model parameters, denoted here as a vector
then only depends on the
model parameters, denoted here as a vector 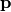 in
parameter space.
in
parameter space.
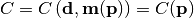
Therefore parameter estimation essentially boils down to finding the
vector of model parameters 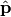 for which the cost
function
for which the cost
function 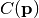 is at its global minimum.
In general this is a multidimensional optimization problem which is
typically solved numerically. There are several algorithms and tools
that can be used for this task:
In kafe2 the Python package SciPy can be used to minimize cost
functions via its
is at its global minimum.
In general this is a multidimensional optimization problem which is
typically solved numerically. There are several algorithms and tools
that can be used for this task:
In kafe2 the Python package SciPy can be used to minimize cost
functions via its scipy.optimize module.
Alternatively, kafe2 can use the MINUIT implementations TMinuit
or iminuit when they are installed.
Choosing a cost function¶
There are many cost functions used in statistics for estimating parameters. In physics experiments two are of particular importance: the sum of residuals and the negative logarithm of the likelihood, which are used in the least squares or the maximum likelihood methods, respectively. Incidentally, these are also the two basic types of cost functions that have been implemented in kafe2.
Least-squares (“chi-squared”)¶
The method of least squares is the standard approach in parameter estimation.
To calculate the value of this cost function the differences between model and
data are squared, then their sum is minimized with respect to
the parameters (hence the name ‘least squares’).
More formally, using the data covariance matrix 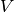 , the cost
function is expressed as follows:
, the cost
function is expressed as follows:
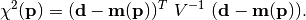
Since the value of the cost function at the minimum follows a 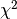 distribution, and therefore the method of least squares is also known as
chi-squared method.
If the uncertainties of the data vector
distribution, and therefore the method of least squares is also known as
chi-squared method.
If the uncertainties of the data vector 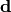 are uncorrelated,
all elements of
are uncorrelated,
all elements of 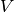 except for its diagonal elements
except for its diagonal elements 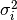 (the squares of the
(the squares of the 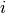 -th point-wise measurement uncertainties) vanish.
-th point-wise measurement uncertainties) vanish.
The above formula then simply becomes
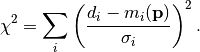
All that is needed in this simple case is to divide the difference between
data 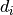 and model
and model 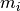 by the corresponding uncertainty
by the corresponding uncertainty 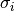 .
.
Computation-wise there is no noticeable difference for small datasets
(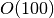 data points). For very large datasets, however, the inversion
of the full covariance matrix takes significantly longer than simply dividing
by the point-wise uncertainties.
data points). For very large datasets, however, the inversion
of the full covariance matrix takes significantly longer than simply dividing
by the point-wise uncertainties.
Negative log-likelihood¶
The method of maximum likelihood attempts to find the best estimation for
the model parameters 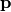 by maximizing the probability with
which such model parameters (under the given uncertainties) would result in the
observed data
by maximizing the probability with
which such model parameters (under the given uncertainties) would result in the
observed data 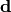 .
More formally, the method of maximum likelihood searches for those values of
.
More formally, the method of maximum likelihood searches for those values of
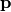 for which the so-called likelihood function of the
parameters (likelihood for short) reaches its global maximum.
for which the so-called likelihood function of the
parameters (likelihood for short) reaches its global maximum.
Using the probability of making a certain measurement given some values of
model parameters 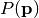 the likelihood function can be defined
as follows:
the likelihood function can be defined
as follows:
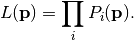
However, usually parameter estimation is not performed by using the likelihood, but by using its negative logarithm, the so-called negative log-likelihood:
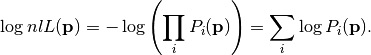
This transformation is allowed because logarithms are
strictly monotonically increasing functions, and therefore
the negative logarithm of any function will have
its global minimum at the same place where the likelihood is maximal.
The parameter values 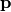 that minimize the negative log-likelihood will
therefore also maximize the likelihood.
that minimize the negative log-likelihood will
therefore also maximize the likelihood.
While the above transformation may seem nonsensical at first, there are important advantages to calculating the negative log-likelihood over the likelihood:
- The product of the probabilities
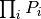 is replaced
by a sum over the logarithms of the probabilities
is replaced
by a sum over the logarithms of the probabilities 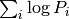 .
This is a numerical advantage because sums can be calculated much more
quickly than products, and sums are numerically more stable than
products of many small numbers.
.
This is a numerical advantage because sums can be calculated much more
quickly than products, and sums are numerically more stable than
products of many small numbers. - Because the probabilities
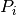 are oftentimes proportional
to exponential functions, calculating their logarithm is actually
faster because it reduces the number of necessary operations.
are oftentimes proportional
to exponential functions, calculating their logarithm is actually
faster because it reduces the number of necessary operations. - Taking the negative logarithm allows for always using the same numerical optimizers to minimize the cost funtions.
As an example, let us look at the negative log-likelihood of data with uncertainties that assume a normal distribution:
![-\log P(\textbf{p})
= - \log \prod_i \frac{1}{\sqrt[]{2 \pi} \: \sigma_i} \exp\left(
\frac{1}{2} \left( \frac{d_i - m_i(\textbf{p})}{\sigma_i} \right)^2\right)
= - \sum_i \log \frac{1}{\sqrt[]{2 \pi} \: \sigma_i} + \sum_i \frac{1}{2}
\left( \frac{d_i - m_i(\textbf{p})}{\sigma_i} \right)^2
= - \log L_\mathrm{max} + \frac{1}{2} \chi^2](../_images/math/e527b03e67e277349d2335ab481bd12897c9ef38.png)
As we can see the logarithm cancels out the exponential function of the normal distribution and we are left with two parts:
The first is a constant part that is represented by 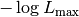 .
This is the minimum value the neg log-likelihood could possibly take on if the
model
.
This is the minimum value the neg log-likelihood could possibly take on if the
model 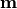 were to exactly fit the data
were to exactly fit the data 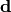 .
.
The second part can be summed up as 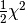 .
As it turns the method of least squares is a special case of the method
of maximum likelihood where all data points have normally distributed uncertainties.
.
As it turns the method of least squares is a special case of the method
of maximum likelihood where all data points have normally distributed uncertainties.