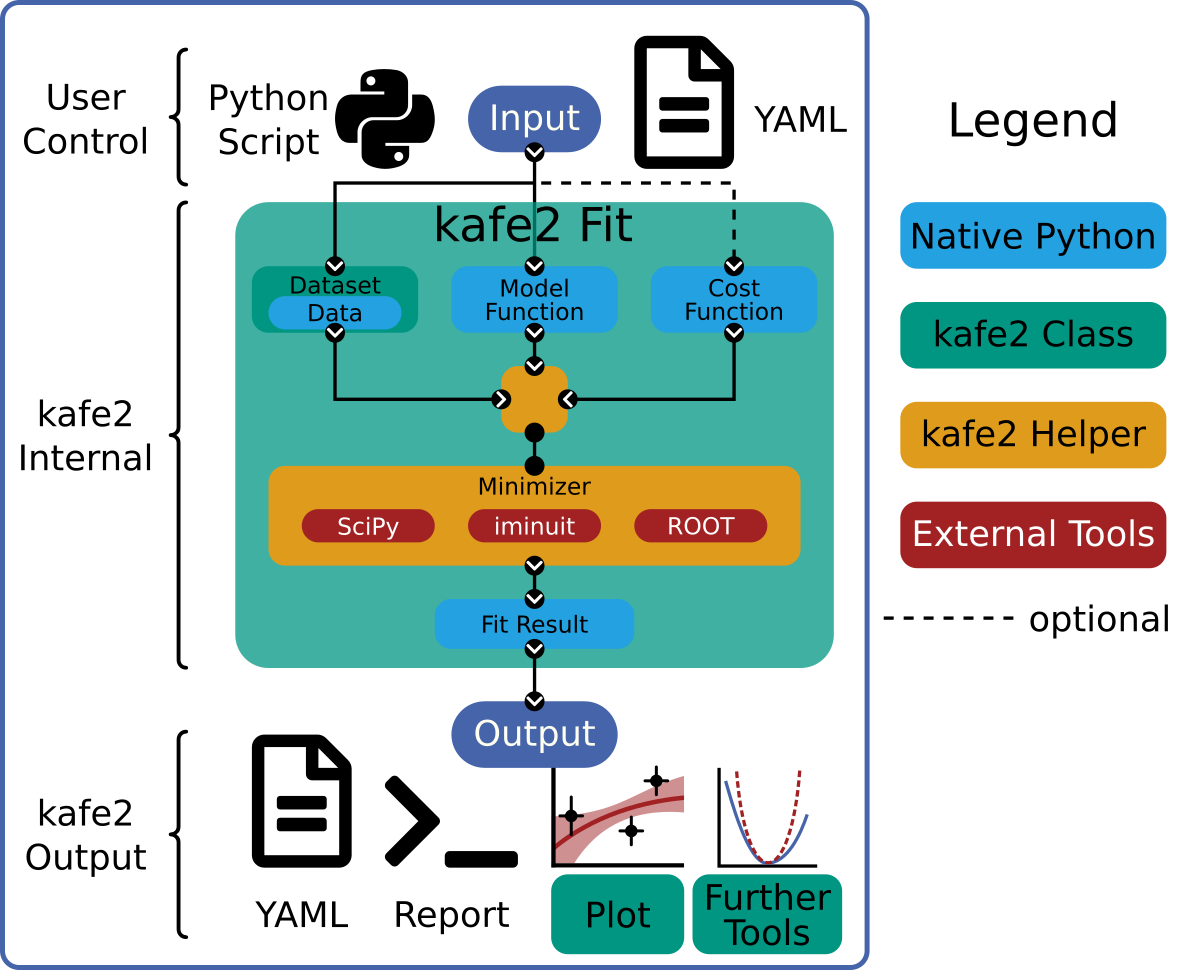
User Guide¶
For performing fits with kafe2, the user need to specify the data, model function and
optionally a cost function to be optimized. Mathematical details are explained
in section Mathematical Foundations.
In most cases the cost function defaults to a negative-log-likelihood
function or, in simple cases or if explicitely requested, the least-squares method.
This information is passed to a FitBase-derived object.
More information can be found in the Fitting-section below.
Then there are multiple ways of displaying and using the fit results. They can either be used directly inside a Python-script, printed to the terminal, or plotted. For further analysis, the Contours Profiler is a very helpful tool to display parameter correlations.
Datasets¶
When performing fits with kafe2, the data is stored in so-called data containers
(DataContainerBase-derived objects).
The difference between the container classes comes down to the type of data they store.
There are two types of data supported by kafe2: One-dimensional data like the lifetimes of particles following a probability density function or two-dimensional data like a current-voltage characteristic.
The most basic example of data is a simple series of one-dimensional data points called indexed data in kafe2 (
IndexedContainer).One-dimensional data can either be kept as-is or filled into a histogram (”binning”). In kafe2 these types of data and their corresponding fits are referred to as unbinned and histogram data/fits (
UnbinnedContainerandHistContainer).Two-dimensional data and the corresponding fit is referred to as XY data/fit (
XYContainer).
Setting the data¶
Data containers are created as regular Python objects from iterables (lists, arrays, etc.) of floats.
XY Container¶
from kafe2 import XYContainer
# Create an XYContainer object to hold the xy data for the fit.
xy_data = XYContainer(x_data=[1.0, 2.0, 3.0, 4.0],
y_data=[2.3, 4.2, 7.5, 9.4])
Unbinned and Indexed Container¶
from kafe2 import IndexedContainer, UnbinnedContainer
idx_data = IndexedContainer([5.3, 5.2, 4.7, 4.8])
unbinned_data = UnbinnedContainer([5.3, 5.2, 4.7, 4.8])
Histogram Container¶
When creating a HistContainer the binning of the histogram has to be determined.
Equidistant bins can be created by using the n_bins and bin_range keywords.
from kafe2 import HistContainer
histogram = HistContainer(n_bins=10, bin_range=(-5, 5))
Alternatively the bin_edges keyword can be used to directly specify bin edges with arbitrary
distances between them:
from kafe2 import HistContainer
hist = HistContainer(bin_edges=[-5.0, -4.0, -3.0, -2.0, -1.0, 0.0, 1.0, 2.0, 3.0, 4.0, 5.0])
After setting the bin edges, the histogram can be filled with data points.
This can be done directly when creating the container with the fill_data keyword or
afterwards with the fill method.
Data points lying outside the bin range will be stored in an underflow or overflow bin and are
not considered when performing the fit.
from kafe2 import HistContainer
histogram = HistContainer(n_bins=10, bin_range=(-5, 5),
fill_data=[-7.5, 1.23, 5.74, 1.9, -0.2, 3.1, -2.75, ...])
# Alternative way
histogram = HistContainer(n_bins=10, bin_range=(-5, 5))
histogram.fill([-7.5, 1.23, 5.74, 1.9, -0.2, 3.1, -2.75, ...])
Instead of filling the histogram with raw data, the bin height can be set manually with
set_bins.
When doing so, rebinning and other options won’t be available.
from kafe2 import HistContainer
histogram = HistContainer(n_bins=5, bin_range=(0, 5))
histogram.set_bins([1, 3, 5, 2, 0], underflow=2, overflow=0)
Data and axis labels¶
The name of the dataset or its label is set with the label property.
Axis labels can be set with the x_label and
y_label properties or the
axis_labels property:
from kafe2 import XYContainer
xy_data = XYContainer(x_data=[1.0, 2.0, 3.0, 4.0], y_data=[2.3, 4.2, 7.5, 9.4])
xy_data.label = 'My Data'
xy_data.axis_labels = ['Time $\\tau$ (µs)', 'My $y$-label']
Text in between dollar signs will be interpreted as latex code. The labels are displayed when plotting the fit results.
Uncertainties¶
To produce a meaningful fit result most cost functions require the user to specify uncertainties. Independent uncertainties and correlated uncertainties are added using the same methods.
Independent uncertainties¶
Independent uncertainties can be added to a dataset (DataContainerBase-derived objects)
with the add_error method:
from kafe2 import XYContainer
x = [19.8, 3.0, 5.1, 16.1, 8.2, 11.7, 6.2, 10.1]
y = [23.2, 3.2, 4.5, 19.9, 7.1, 12.5, 4.5, 7.2]
data = XYContainer(x_data=x, y_data=y)
data.add_error(axis='x', err_val=0.3) # +/-0.3 for all data points in x-direction
data.add_error(axis='y', err_val=0.15, relative=True) # +/-15% for all points in y-direction
The axis keyword is is only used with XYContainers for the add_error
method.
If err_val is a single float the same uncertainty is applied to all data points.
If err_val is a list of floats with the same length as the corresponding data,
each entry in err_val is applied to the data point with the same index.
Fitting¶
Creating the correct FitBase derived object can simply be done with the
Fit function, which automatically determines the correct fit type for a
DataContainerBase derived object:
from kafe2 import XYContainer, Fit
xy_data = XYContainer(x_data=[1.0, 2.0, 3.0, 4.0],
y_data=[2.3, 4.2, 7.5, 9.4])
# Create an XYFit object from the xy data container.
# By default, a linear function f=a*x+b will be used as the model function.
line_fit = Fit(data=xy_data)
# further additions like constraints go here
line_fit.do_fit()
Alternatively XYFit, HistFit, UnbinnedFit or
IndexedFit can be used to create fits with corresponding datasets.
Warning
Always run the do_fit function of the Fit object when everything is set.
Only when calling this function the fit will be performed.
Setting a model function¶
kafe2 fit objects accept normal Python functions as model functions.
The first parameter of those functions will be used as the independent parameter
(the parameter on the x axis of plots).
The default parameter values of the Python function will be used as starting values for the fit,
unless overwritten with the set_parameter_values method.
def linear_model(x, a, b):
# Our first model is a simple linear function
return a * x + b
def exponential_model(x, A0=1., x0=5.):
# Our second model is a simple exponential function
# The kwargs in the function header specify parameter defaults.
return A0 * np.exp(x/x0)
xy_data = XYContainer(x_data=[1.0, 2.0, 3.0, 4.0],
y_data=[2.3, 4.2, 7.5, 9.4])
# Create 2 Fit objects with the same data but with different model functions
linear_fit = Fit(data=xy_data, model_function=linear_model)
exponential_fit = Fit(data=xy_data, model_function=exponential_model)
The display names for the model function and its parameters can be changed like this:
linear_fit.assign_model_function_name("line")
linear_fit.assign_parameter_names(a='A', b='b', x='t')
linear_fit.assign_model_function_expression("{a}{x} + {b}")
exponential_fit.assign_model_function_latex_name("\\exp")
exponential_fit.assign_parameter_latex_names(A0='A_0', x0='x_0', x='\\tau')
exponential_fit.assign_model_function_latex_expression("{A0} e^{{{x}/{x0}}}")
The latex parameter names and expressions define the graphical output when plotting while the non latex methods define the output names when reporting the fit results to the terminal.
Note
Special characters inside the strings need to be escaped. E.g. a single \ needs to be
\\.
Note
Inside the latex expression string, { and } for latex expressions like \\frac
need to be doubled, because single curly brackets are used for replacing the parameters with
their respective latex names.
E.g. kafe2 tries to replace {x0} with its latex string x_0 in this example.
Parameter Constraints¶
When performing a fit, some values of the model function might have already been determined in previous experiments. Those results and uncertainties can then be used to constrain the given parameters in a new fit. This eliminates the need to manually propagate the uncertainties on the final fit results, as it’s now done numerically.
Simple parameter constraints are set with the add_parameter_constraint method:
# Constrain model parameters to measurements
fit.add_parameter_constraint(name='l', value=l, uncertainty=delta_l)
fit.add_parameter_constraint(name='r', value=r, uncertainty=delta_r)
fit.add_parameter_constraint(name='y_0', value=y_0, uncertainty=delta_y_0, relative=True)
Note
The names have to be identical to the argument names in the model function. The parameter
names can be accessed with the fit parameter_names property.
If the uncertainties of several parameter constraints are correlated the
add_matrix_parameter_constraint method can be used instead.
Please refer to the API Documentation for more information.
Fixing and limiting parameters¶
Limiting the parameters of a model function can be useful for improving the convergence of a fit by reducing the size of the parameter space in which it searches for the global cost function minimum. This is commonly done when the fit result of one or more parameters is expected to fall in a certain range or when the model function is not valid for some parameter values (e.g. a negative amplitude). For fits with many parameters fixing some of them at first and fitting multiple times might also help.
Fixing parameters is done with the fix_parameter method and limiting with the
limit_parameter method. Releasing a fixed parameter is performed with
release_parameter and unlimiting a parameter with
unlimit_parameter:
fit.fix_parameter("a", 1)
fit.fix_parameter("b", 11.5)
fit.release_parameter("a")
# limit parameter fbg to avoid unphysical region
fit.limit_parameter("fbg", 0., 1.)
fit.unlimit_parameter("fbg")
Note
The names have to be identical to the argument names in the model function. The parameter
names can be accessed with the fit parameter_names property.
Fixed parameters can be released with the release_parameter method and
limited parameters can be unlimited with the unlimit_parameter method.
Minimizers¶
Currently the use of three different minimizers is supported. By default iminuit is
used. If iminuit is not available, kafe2 falls back to
scipy.optimize.minimize.
The usage of a specific minimizer can be set during initialization of any
FitBase-object with the minimizer keyword.
Depending on the installed minimizers this can either be 'iminuit', 'scipy' or
'root'.
Additional keywords for the instantiation can be passed as a dict via the
minimizer_kwargs keyword when creating a fit object derived from FitBase.
Logging¶
To enable the output of the minimizer, set up a logger before calling do_fit:
import logging
logger = logging.getLogger()
logger.setLevel(logging.INFO)
This currently only works for the scipy and iminuit minimizer.
For more detailed information increase the logging level to logging.DEBUG.
This will give a more verbose output when using iminuit.
The logger level should be reset to logging.WARNING before plotting.
Otherwise matplotlib will create logging messages as well.
Access the fit results¶
The do_fit method returns a dictionary containing most of the relevant
results. Additionally the results can be printed to the terminal with report.
The parameter values can also be accessed via the parameter_values property
as well as the symmetric and asymmetric parameter uncertainties and the correlation and
covariance matrices via their respective properties:
fit = Fit(my_dataset) # create a fit object
# perform the fit and calculate asymmetric uncertaintes
result = fit.do_fit(asymmetric_parameter_errors=True)
fit.report() # print fit results to the terminal
par_vals = fit.parameter_values
par_errs = fit.parameter_errors
par_errs_asym = fit.asymmetric_parameter_errors
par_ocv_mat = fit.parameter_cov_mat
par_cor_mat = fit.parameter_cor_mat
A typical dictionary returned by the do_fit method looks like this:
{'did_fit': True,
'cost': 1.7759115950075888,
'ndf': 2,
'goodness_of_fit': 1.7759115950075888,
'cost/ndf': 0.8879557975037944,
'chi2_probability': 0.41149607486886164,
'parameter_values': OrderedDict([('a', 2.468773761415478), ('b', -0.3219331193129483)]),
'parameter_cov_mat': array([[ 0.0443453 , -0.1108627 ],
[-0.1108627 , 0.33239252]]),
'parameter_errors': OrderedDict([('a', 0.2105624096609012), ('b', 0.576478065203752)]),
'parameter_cor_mat': array([[ 1. , -0.9131448],
[-0.9131448, 1. ]]),
'asymmetric_parameter_errors': None}
Plotting¶
For displaying the results of a Fit, kafe2 provides a Plot-class. In the background
a matplotlib.pyplot.figure-object is created. This means that all customization possible
with Matplotlib can be done with kafe2-Plots as well.
The Plot class supports plotting multiple fits at once. By default they will all appear in the same figure. The keyword separate_figures=True changes this behaviour, so that each fit will be plotted to a separate figure.
import matplotlib.pyplot as plt
from kafe2 import Plot
p = Plot([fit_1, fit_2])
# for separate figures use:
# p = Plot([fit_1, fit_2], separate_figures=True)
# insert customization here
p.plot()
plt.show()
Running the plot function will perform the the plot. Customization should be
done before this. After plotting the fits, the according matplotlib objects can be
accessed via the figures and axes properties.
Customize the Plot¶
Note
The plot method must be called after all customization is done. Otherwise
not all customizations will appear in the plot.
Axis Range¶
The plot range can be set via the x_range and y_range
properties:
# set the same range for all plots
p.x_range = (0, 10)
p.y_range = (-5, 25)
# set different ranges for each plot, the length must match the number of fits handled by the
# plot object.
p.x_range = [(0, 10), (-5, 5)]
p.y_range = [(-5, 25), (10, 100)]
p.plot() # plot method must come after the customization
Axis Scale¶
Additionally the axis scale can be changed to logarithmic. When changing between a linear and logarithmic x-axis scale, the supporting points for plotting the model function will be updated and evenly spaced on a linear or logarithmic scale.
# set the same scale for all fits in this plot object
p.x_scale = "log"
p.y_scale = "linear
# or change the scale for each fit individually
# only use this when `separate_figures=True` is set in the Plot constructor
p.x_scale = ["linear", "log"]
p.y_scale = ["log", "log"]
p.plot() # plot method must come after the customization
Axis Labels¶
By default, the plot will use the labels specified for each dataset (see Data and axis labels). If multiple fits are plotted to the same figure, the axis labels from the data containers are concatenated while skipping duplicates.
Alternatively the axis labels can be overwritten for each fit. Again if multiple fits are plotted to the same figure, all labels will be concatenated while skipping duplicates.
# set the same axis labels for all fits in this plot object
p.x_label = "My $x$-label"
p.y_label = "Voltage [mV]"
# set different labels for each fit, the length must match the number of fits
p.x_label = ["$x_1$", "My other label for $x_2$"]
p.y_label = ["$Y_1$", "$y_2$"]
p.plot() # plot method must come after the customization
Plot Style¶
Each graphic element has it’s own plotting method and can be customized individually. Available
plot_types for XYFits are
'data', 'model_line', 'model_error_band', 'ratio', 'ratio_error_band' and ‘model’ which
is hidden by default.
The plot_types may differ for different types of fits.
The currently set keywords can be obtained with the get_keywords method.
With customize new values can be added or existing values can
be modified. Using '__del__' will delete the keyword and '__default__' will reset
it.
Hiding specific elements from the plot (e.g. the uncertainty band) is done like this:
# the array length must match the amount of fits handled by this plot object.
p.customize('model_error_band', 'hide', [True])
In order to change the name for the data set and suppress the second output, use the following call:
p.customize('data', 'label', [(0, "test data"), (1, '__del__')])
Marker type, size and color of the marker and error bars can also be customized:
p.customize('data', 'marker', [(0, 'o'), (1,'o')])
p.customize('data', 'markersize', [(0, 5), (1, 5)])
p.customize('data', 'color', [(0, 'blue'), (1,'blue')]) # note: although 2nd label is suppressed
p.customize('data', 'ecolor', [(0, 'blue'), (1, 'blue')]) # note: although 2nd label is suppressed
The corresponding values for the model function can also be customized:
p.customize('model_line', 'color', [(0, 'orange'), (1, 'lightgreen')])
p.customize('model_error_band', 'label', [(0, r'$\pm 1 \sigma$'), (1, r'$\pm 1 \sigma$')])
p.customize('model_error_band', 'color', [(0, 'orange'), (1, 'lightgreen')])
Additionally it is possible to change parameters using matplotlib functions. Changing the size of the axis labels is done with the following calls:
import matplotlib as mpl
mpl.rc('axes', labelsize=20, titlesize=25)
Contours Profiler¶
Todo
Add this section, examples already use the contours profiler.